本文字数为 905 字, 预计读完大约需要 3 分钟

吴恩达人工智能课程第二周笔记二：偏差、方差

概念

在机器学习中，很少谈及偏差和方差的均衡问题，通常都是将它们两个分开来考虑

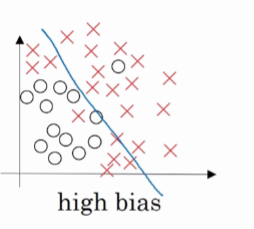高偏差在这个例子中，拟合的直线不能很好的拟合数据，我们称这个拟合的直线偏差较高，我们称为欠拟合。

高方差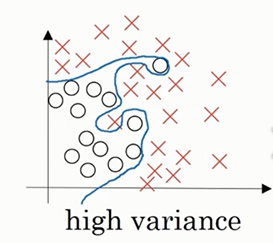比如在含有隐藏层的网络中，我们可以拟合出上图的曲线来，但是这个曲线看起来不错，其实不然，我们说这样的曲线方差较高，数据过度拟合，因为可以看到，对于数据中的极个别的点，曲线也去拟合，将会导致整体数据方差增大。

较合理的拟合结果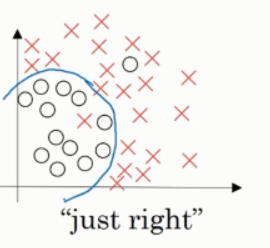这样的拟合曲线看起来就更加合理，我们称之为适度拟合，是介于过拟合和欠拟合中间的一类

上面的实例中，我们对于数据的维度是二维，因为这样可以可视化数据的拟合曲线，但是现实中的数据要比二维大，我们没有办法去查看数据的拟合情况，该怎么来知道数据的偏差和方差，来判断数据模型是否欠拟合还是过拟合呢？

理解偏差和方差的两个关键数据是训练集误差和验证集误差。下面以训练集误差和开发集误差的不同结果作为解释。

不同训练误差和验证误差分析：

Train Set Error（训练集误差）	1%	15%	15%	0.5%
Dev Set Error（验证集误差）	11%	16%	30%	1%
假设人的误差在0~1%	我们可以看到对训练集误差很小，而对开发集的误差却很大，这种情况我们称之为对训练集“过拟合”，也称之为高方差	这里数据的拟合并不好，但是可以看到开发集和训练集很接近，因此可以判断这个数据为高偏差	这种情况，训练集的训练结果不理想，同时开发集和训练集的误差相差很大，我们称为高偏差和高方差	这种情况数据的拟合情况就很好，偏差很低方差也很低

上面的误差分析是在我们人类的误差基础上进行分析的数据，假设是0%~1%，也就是最优误差是0%~1%（也称贝叶斯误差）。假如我们人类的误差是15%，那么情况就有所不同，上面的第二种情况不会是高偏差的情况了，而是偏差方差都适中的情况了。